솜은 코튼
[NW] 아날로그 신호 (주기, 주파수, 대역폭) 본문
주기와 주파수
.


아날로그 신호는 부드럽게 변화하는 연속적인 파형이며,
디지털 신호는 이산적이며 1, 0과 같이 제한된 수의 정의된 값만 가질 수 있다.
주기 신호는 특정 패턴을 갖추고 나서 그 이후 동일한 주기에 동일한 패턴이 반복된다.
하나의 완성된 패턴은 사이클이라 부른다.

위의 그림은 정현파이며, 위상과 주파수는 같지만 진폭이 다른 2개의 신호이다.
'정현파'는 한 사이클을 진행하는 동안의 변화는 일정하며 연속적으로 흘러가는 흐름을 지닌다.
정현파는 최대 진폭, 주파수, 위상이라는 세 가지 특성으로 나타낸다.
'주기'는 신호가 한 사이클을 완성하는 데 필요한 시간의 양을 나타낸다.
'주파수'란 1초 동안 생성되는 신호 주기의 수를 말한다.
'위상'은 시각 0시에 대한 파형의 상대적인 위치를 기술한다.
주기는 주파수의 역이고, 주파수는 주기의 역이다.
f = 1/T, T = 1/f
주기와 주파수 단위는 아래와 같다.

예로, 100ms의 주기를 마이크로초로 나타내면
100ms = 100 X 10^(-3)s
10^(-6)을 만들어 주어야 하므로
10^(-3) X 10^(3)을 곱해서
100 X 10^(3) X µs
즉, 10^(5)µs가 된다.
한 신호의 주기가 100ms일 때 주파수는
100 X 10^(-3)s = 10^(-1)s
f = 1/10^(-1) = 10Hz 가 된다.
만약 kHz로 바꾼다면
10^(-3) X 10^(3)을 곱해서
10^(-2) kHz가 된다.
40Hz 신호의 주파수는 80Hz 신호에 비해 두 배의 시간이 걸린다.
즉, 주파수는 시간에 대한 짧은 시간 내의 변화는 높은 주파수를 의미하고
긴 시간에 걸친 변화는 낮은 주파수를 의미한다.
대역폭
.

복합 신호는 여러 개의 단순 정현파로 만들어진다.
위의 그림은 비주기 복합 신호의 그림이다.
복합 신호를 시간 영역에서 표시하면(a) 무한개의 단순 정현파로 나타난다.
신호의 주파수 분해는(b) 연속된 곡선으로 표시된다.
0.0과 4000.0 사이의 무한개의 주파수로 표시된다.

위의 그림은 복합 주기 신호의 시간 영역 및 주파수 영역을 분해한 것이다.
복합 신호에 포함된 주파수 영역을 '대역폭'이라고 한다.
예를 들어 어느 복합 신호가 주파수 1000부터 5000까지 포함한다면
대역폭은 5000-1000으로 4000이 된다.
즉, 복합 신호의 대역폭은 신호에 포함된 최고 주파수와 최저 주파수의 차이이다.
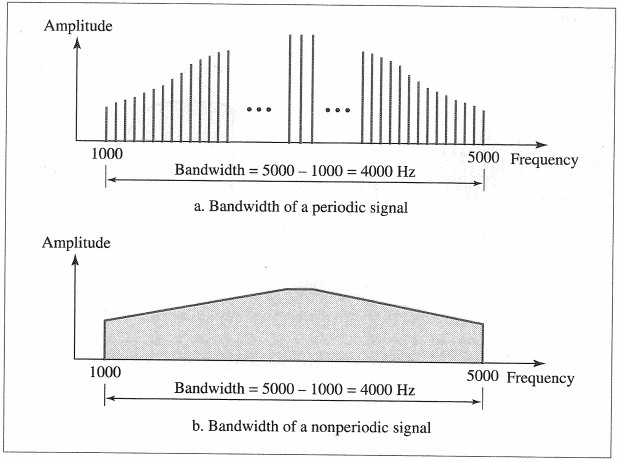
위의 그림은 주기 신호와 비주기 신호의 두 복합 신호가 있다.
주기 신호의 대역폭은 1000부터 5000까지의 모든 정수 주파수를 담고 있다.
비주기 신호의 대역폭도 같은 영역에 있지만 주파수는 연속적이다.
만약 주기 신호가 주파수 100, 300, 500, 700, 900Hz를 갖는 5개의 정현파로 분해되며,
모든 구성요소가 10V의 최대 진폭을 갖는다고 가정한다.
이때 대역폭과 스펙트럼을 그려보면 아래와 같이 5개 막대만을 가진다.

어떤 신호가 20Hz의 대역폭을 가지며, 최고 주파수는 60Hz이면
가장 낮은 주파수는 60 - 20 = 40Hz이다.
신호가 같은 진폭의 모든 정수 주파수를 포함할 때 스펙트럼을 그린다면
아래와 같이 연속적인 막대들이 그려진다.

어느 비주기 복합 신호의 대역폭이 200kHz이며, 그 중간 지점은 140kHz이고,
최대 진폭은 20V다. 양 극단의 주파수에서의 진폭은 0이다.
이 신호의 주파수 영역을 그린다면 아래와 같다.

* 해당 글은 '데이터통신과 네트워킹' 책을 참고하여 작성하였습니다. 출처: 데이터통신과 네트워킹 5 (Forouzan)
'NW' 카테고리의 다른 글
| [NW] 다중화 (시분할 다중화) (0) | 2023.06.04 |
|---|---|
| [NW] 다중화 (주파수 분할 다중화) (0) | 2023.06.04 |
| [NW] 디지털 전송 (디지털 변환, 표본 채집률, 부호화) (0) | 2023.06.04 |
| [NW] 대역폭, 처리율, 지연, 대역폭-지연 곱 (0) | 2023.06.04 |
| [NW] 디지털 신호 (비트율, 전송장애, 데이터 전송률) (1) | 2023.06.04 |




